Goal is to win the game in min dice throws.We will calculate the required the number of throws and the most optimal path.
Prerequisites : Graph Basics , Breadth First Search
Overview
Let’s take the following Snakes and Ladders Game as example.The starting point is 0 , we need to reach 36 in min number of moves.Just think how can we solve it ? Hint : Answer lies in the graph theory.
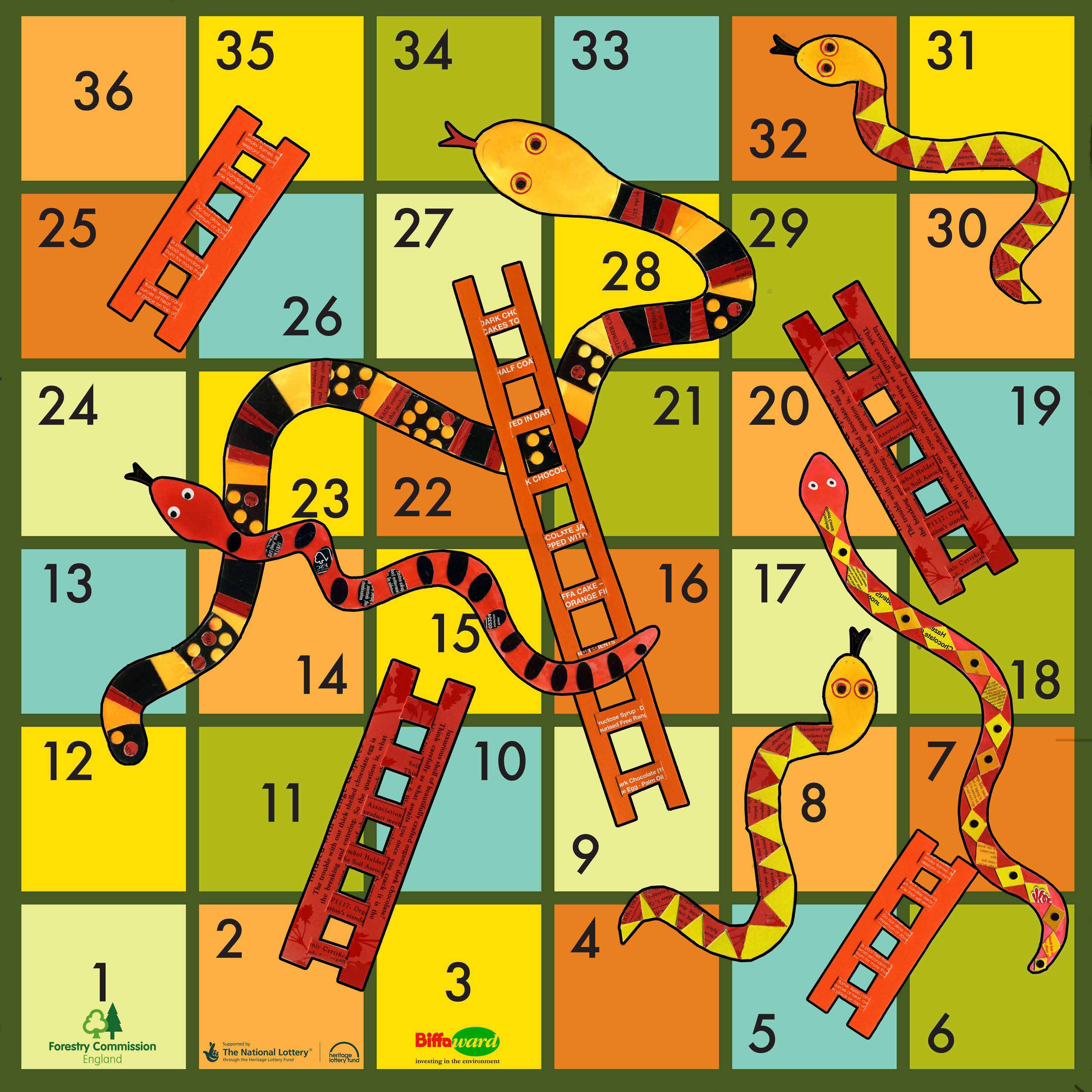
Question 1 : Can we visualise the following game as a graph ?
The answer is Yes, It is a directed graph where possible move is an edge. Think of Move 1->2 , 3->4 as edges , similarly Ladder Climbing Move 2->15 as an edge, and Snake Biting Move 24->16 as an edge and so on …
Question 2 : How to store this Graph ?
Well,we can make an adjacency list out of it but wait , there is an easier way to do it. We can simply use an 1-Dimensional Linear Array for it. Surprised ? Lets see how.
Consider an array of length equal to gridsize.At each position in the array we can store the POSITION to which that index will take. OR we can simply store the increment in the position from that index. Like ladder starting point index will have a positive increment , snake bite position will have Negative Value and rest all positions will have a possilbe range of increments between 1-6.
###Question 3 : Dijkshtra’s or BFS ?
Since every edge has same weight (taking 1 here) as every move occurs with one die throw , so we can use BFS to calculate the shortest path (min edges and throws) to reach it.Go ahead and Code !
###Let’s Code !
####### Any Doubts ? Feel free to DISQUS below …
